Giải Bài 35 SBT Toán 8 Tập 1 Trang 84

Đào Huệ 12/06/2024

279 1 minute read

Trong bài viết dưới đây Trường kinh doanh công nghệ sẽ hướng dẫn bạn giải đáp Bài 35 SBT Toán 8 Tập 1 trang 84. Mời bạn đọc cùng theo dõi!

Nội dung Bài 35 SBT Toán 8 Tập 1 Trang 84

Hình thang ABCD có đáy AB, CD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng ba điểm E, F, I thắng hàng.

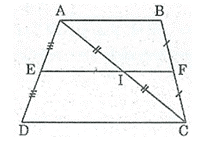
Lời giải:

Hình thang ABCD có AB // CD

E là trung điểm của AD và F là trung điểm của BC (gt)

Nên EF là đường trung bình của hình thang ABCD

EF // CD (tính chất đường trung bình hình thang) (1)

Trong ΔADC ta có:

E là trung điểm của AD và I là trung điểm của AC (gt)

Nên EI là đường trung bình của ΔADC

⇒ EI // CD (tính chất đường trung bình tam giác) (2)

Từ (1) và (2) và theo tiên đề Ơ-clít ta có đường thẳng EF và EI trùng nhau.

Vậy E, F, I thẳng hàng.

Trên đây là hướng dẫn giải Bài 35 Sbt Toán 8 Tập 1 trang 84, cùng với đó là kiến thức liên quan mà Truongkinhdoanhcongnghe tổng hợp được và chia sẻ tới bạn. Hi vọng bài viết sẽ hữu ích với bạn, chúc bạn học tập tốt!

Xem thêm:

Đào Huệ

Tốt nghiệp khoa sư phạm tiểu học, nhiều năm trực tiếp giảng dạy bậc tiểu học, cô rất hiểu tâm lý các em HS; lối truyền đạt kiến thức phù hợp với con trẻ. Với quan điểm “Giáo dục là vũ khí mạnh nhất để thay đổi cả thế giới” cô Huệ luôn cố gắng hết mình để truyền tải tri thức tới các em học sinh.

Đào Huệ 12/06/2024

279 1 minute read