


Trong bài viết dưới đây Trường kinh doanh công nghệ sẽ hướng dẫn bạn giải đáp Bài 49 SGK Toán 8 Tập 1 Trang 93. Mời bạn đọc cùng theo dõi!

Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
a) AI // CK
b) DM = MN = NB
Phương pháp giải:
Sử dụng các kiến thức về:
Lời giải:
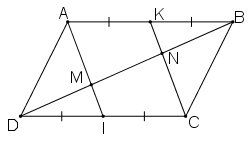
a) Ta có: K là trung điểm của AB ⇒AK=AC/2
Ta có: I là trung điểm của CD ⇒CI=CD/2
Vì ABCD là hình bình hành
⇒ AB // CD hay AK // CI
và AB = CD hay AK = CI
Xét tứ giác AKCI có AK // CI và AK = CI
⇒ AKCI là hình bình hành.
b) Vì AKCI là hình bình hành
⇒ AI//KC hay MI//NC.
Xét ΔDNC có:
I là trung điểm DC
IM // NC
⇒ M là trung điểm DN
⇒ DM = MN (1)
Xét ΔBAM có:
K là trung điểm AB
KN//AM
⇒ N là trung điểm BM
⇒ MN = NB (2)
Từ (1) và (2) suy ra DM = MN = NB.
Trên đây là hướng dẫn giải Bài 49 SGK Toán 8 Tập 1 Trang 93, cùng với đó là kiến thức liên quan mà Truongkinhdoanhcongnghe tổng hợp được và chia sẻ tới bạn. Hi vọng bài viết sẽ hữu ích với bạn, chúc bạn học tập tốt!