

Trong bài viết dưới đây Trường kinh doanh công nghệ sẽ hướng dẫn bạn giải đáp Bài 27 Sgk Toán 9 Tập 1 Trang 115. Mời bạn đọc cùng theo dõi!

Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.

Sử dụng tính chất hai tiếp tuyến cắt nhau: cho (O;R) với hai tiếp tuyến AB, AC tại B, C của (O) khi đó AB=AC
Chu vi tam giác ABC là: CΔABC=AB+BC+AC.
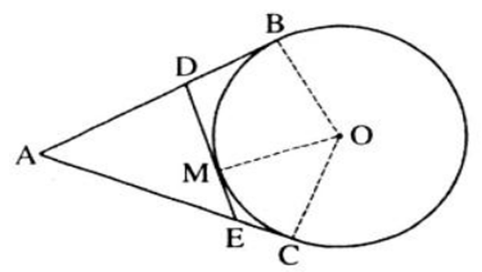
Vì AB, AC là hai tiếp tuyến của (O) lần lượt tại B, C. Theo tính chất của hai tiếp tuyến cắt nhau, ta có: AB=AC
Vì DB, DM là hai tiếp tuyến của (O) lần lượt tại B, M. Theo tính chất của hai tiếp tuyến cắt nhau, ta có: DB=DM
Vì EM, EC là hai tiếp tuyến của (O) lần lượt tại M, C. Theo tính chất của hai tiếp tuyến cắt nhau, ta có: EM=EC
Chu vi tam giác ADE là: AD+DE+EA=AD+(DM+ME)+EA
=(AD+DM)+(ME+EA)
=(AD+DB)+(EC+EA) (vì DM=DB và ME=EC)
=AB+AC=2AB=2AB (vì AC=AB).
Nếu 2 tiếp tuyến của 1 đường tròn cắt nhau tại 1 điểm thì ta rút ra được các tính chất sau:
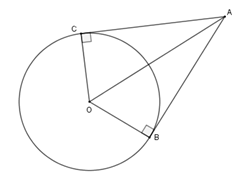
Ví dụ minh họa: Đối với đường tròn tâm O có 2 điểm B, C nằm trên đường tròn. Từ B và C kẻ các tiếp tuyến và chúng cắt nhau tại A.
Áp dụng tính chất của 2 tiếp tuyến cắt nhau: Ta dễ dàng rút ra được kết luận như sau:
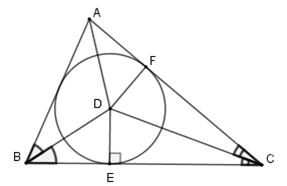
Khi đường tròn tiếp xúc với ba cạnh của cùng một tam giác, lúc đó được gọi là đường tròn nội tiếp tam giác hay nói cách khác: tam giác ấy ngoại tiếp đường tròn.
Cách xác định tâm của đường tròn nội tiếp tam giác: Ta tìm giao điểm của các đường phân giác các góc trong tam giác.

Khái niệm đường tròn bàng tiếp tam giác là gì: Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với phần kéo dài của hai cạnh còn lại gọi là đường tròn bàng tiếp tam giác. Với một tam giác có ba đường tròn bàng tiếp, tương ứng với 3 giao điểm của cạnh và phần kéo dài của 2 cạnh còn lại.
Cách xác định tâm của đường tròn bàng tiếp tam giác: Ta cần tìm giao điểm của 1 đường phân giác trong và 2 đường phân giác ngoài của tam giác
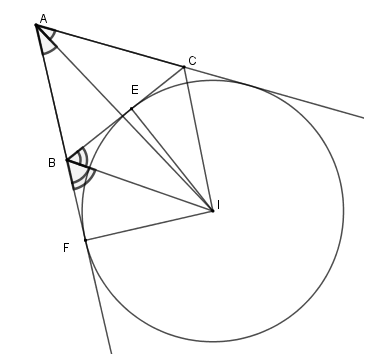
Ví dụ minh họa:

Nhìn vào hình vẽ, ta thấy rằng tâm của đường tròn bàng tiếp tam giác trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, hoặc là giao điểm của đường phân giác góc A và đường phân giác góc ngoài tại B (hoặc C). Với tam giác ABC này, ta dễ dàng tìm được 3 đường tròn bàng tiếp.
Trên đây là hướng dẫn giải Bài 27 Sgk Toán 9 Tập 1 Trang 115, cùng với đó là kiến thức liên quan mà Truongkinhdoanhcongnghe tổng hợp được và chia sẻ tới bạn. Hi vọng bài viết sẽ hữu ích với bạn, chúc bạn học tập tốt!
Xem thêm: