ByDao Hue
Tìm Hiểu Về Phương Trình Đi Qua 2 Điểm Cực Trị
Share your love
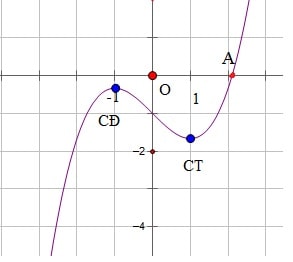
Trong toán học, việc tìm Phương Trình Đi Qua 2 Điểm Cực Trị trên một đồ thị là một kỹ thuật quan trọng để phân tích và mô tả hình dạng của một hàm số. Điều này đặc biệt hữu ích trong các ứng dụng thực tế như tối ưu hóa, phân tích dữ liệu và mô hình hóa các quá trình vật lý.
Trong bài viết này, Trường Kinh doanh Công nghệ sẽ tìm hiểu cách xác định phương trình của đường thẳng đi qua hai điểm cực trị của một hàm số. Chúng ta sẽ thảo luận về các bước cần thực hiện, cung cấp ví dụ minh họa và phân tích ứng dụng của kỹ thuật này.
Tìm Điểm Cực Trị
Trước tiên, chúng ta cần xác định các điểm cực trị của hàm số. Điểm cực trị là những điểm trên đồ thị của hàm số tại đó hàm số đạt giá trị lớn nhất (cực đại) hoặc nhỏ nhất (cực tiểu).
Để tìm các điểm cực trị, chúng ta có thể sử dụng các phương pháp như:
- Phân tích hàm số: Tìm các điểm mà đạo hàm của hàm số bằng 0 hoặc không tồn tại. Các điểm này có thể là điểm cực trị.
- Vẽ đồ thị: Vẽ đồ thị của hàm số và xác định các điểm cực đại và cực tiểu trên đồ thị.
- Sử dụng công thức tính toán: Đối với một số hàm số đơn giản, chúng ta có thể sử dụng các công thức toán học để tính trực tiếp các điểm cực trị.
Sau khi xác định được các điểm cực trị, chúng ta có thể tiến hành tìm phương trình đường thẳng đi qua hai điểm này.
Xác Định Phương Trình Đường Thẳng
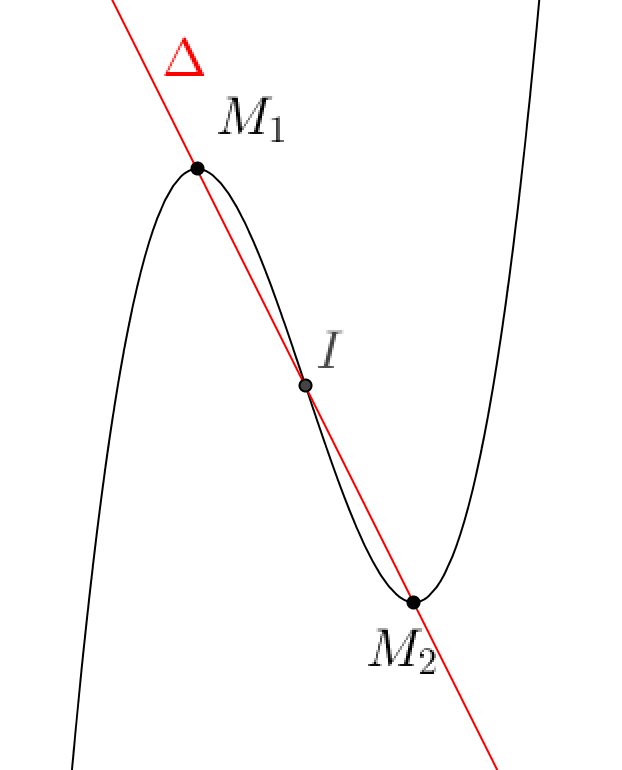
Giả sử chúng ta có hai điểm cực trị (x1, y1) và (x2, y2). Để tìm phương trình đường thẳng đi qua hai điểm này, chúng ta sử dụng công thức:
Phương trình đường thẳng: y = mx + b
Trong đó:
- m là hệ số góc của đường thẳng
- b là tọa độ điểm cắt trục y
Để tìm m và b, chúng ta sử dụng các công thức sau:
- Tính hệ số góc m: m = (y2 – y1) / (x2 – x1)
- Tính tọa độ điểm cắt trục y b: b = y1 – m * x1 hoặc b = y2 – m * x2
Như vậy, phương trình đường thẳng đi qua hai điểm cực trị (x1, y1) và (x2, y2) sẽ là: y = m*x + b
Trong đó:
- m = (y2 – y1) / (x2 – x1)
- b = y1 – mx1 hoặc b = y2 – mx2
Hãy xem xét ví dụ sau để hiểu rõ hơn về quá trình này.
Ví Dụ Minh Họa
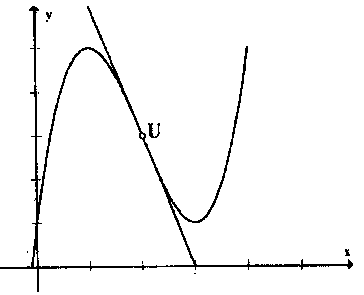
Giả sử chúng ta có một hàm số f(x) = x^3 – 6x^2 + 9x – 4. Chúng ta muốn tìm phương trình đường thẳng đi qua hai điểm cực trị của hàm số này.
Bước 1: Tìm các điểm cực trị của hàm số. Để tìm các điểm cực trị, chúng ta cần tính đạo hàm của hàm số: f'(x) = 3x^2 – 12x + 9
Sau đó, chúng ta tìm các điểm mà đạo hàm bằng 0 hoặc không tồn tại: 3x^2 – 12x + 9 = 0 (3x – 9)(x – 1) = 0 x = 3 hoặc x = 1
Vậy, các điểm cực trị của hàm số là (1, 4) và (3, -10).
Bước 2: Tính phương trình đường thẳng đi qua hai điểm cực trị. Áp dụng công thức, chúng ta có: m = (y2 – y1) / (x2 – x1) m = (-10 – 4) / (3 – 1) m = -14 / 2 m = -7
Tiếp theo, chúng ta tính b: b = y1 – m*x1 b = 4 – (-7)*1 b = 11
Vậy, phương trình đường thẳng đi qua hai điểm cực trị (1, 4) và (3, -10) là: y = -7x + 11
Như vậy, chúng ta đã tìm được phương trình đường thẳng đi qua hai điểm cực trị của hàm số f(x) = x^3 – 6x^2 + 9x – 4.
Kết Luận
Trong bài viết này, Trường Kinh doanh Công nghệ đã tìm hiểu cách xác định phương trình đi qua hai điểm cực trị của một hàm số. Chúng ta đã thảo luận về các bước cần thực hiện, cung cấp ví dụ minh họa và phân tích ứng dụng của kỹ thuật này trong thực tế.
Xem thêm:
