Cách Giải Các Phương Trình Đưa Được Về Dạng Ax B 0
Share your love
Trong bài viết dưới đây trường kinh doanh công nghệ sẽ hướng dẫn bạn đọc cách giải các phương Trình Đưa Được Về Dạng Ax B 0. Mời bạn đọc cùng theo dõi!
Chi tiết cách giải Phương Trình Đưa Được Về Dạng Ax B 0
Để giải các phương trình đưa được về ax+b=0 ta thường biến đổi phương trình như sau:
- Quy đồng mẫu hai vế và khử mẫu.
- Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng ax+b=0 hoặc ax=−b
- Tìm x
Chú ý: Quá trình biến đổi phương trình về dạng ax+b=0 có thể dẫn đến trường hợp đặc biệt là hệ số a=0 nếu:
- 0x=−b (b≠0) thì phương trình vô nghiệm S=ϕ
- 0x=0 thì phương trình nghiệm đúng với mọi x hay vô số nghiệm: S=R.
Kiến thức liên quan về Phương Trình Đưa Được Về Dạng Ax B 0
- Ví dụ 1: Giải phương trình 2x – (3 – 2x) = 3x + 1
Hướng dẫn:
Ta có 2x – (3 – 2x) = 3x + 1 ⇔ 2x – 3 + 2x = 3x + 1
⇔ 4x – 3x = 1 + 3 ⇔ x = 4.
Vậy phương trình đã cho có tập nghiệm là S = {4}.
- Ví dụ 2: Giải phương trình
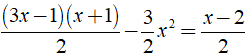
Hướng dẫn:
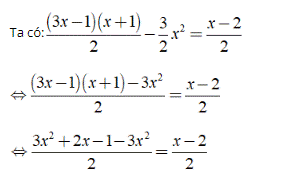
⇔ 2x – 1 = x – 2 ⇔ x = – 1.
Vậy phương trình đã cho có tập nghiệm là S = { – 1 }.
- Ví dụ 3: Giải phương trình x + 1 = x – 1.
Hướng dẫn:
Ta có x + 1 = x – 1 ⇔ x – x = – 1 – 1 ⇔ 0x = – 2.
Vậy phương trình đã cho vô nghiệm.
- Ví dụ 4: Giải phương trình x – 3 = x – 3.
Hướng dẫn:
Ta có: x – 3 = x – 3 ⇔ x – x = – 3 + 3 ⇔ 0x = 0.
Vậy phương trình đã cho vô số nghiệm.
Định nghĩa phương trình bậc nhất một ẩn
Phương trình dạng ax + b = 0 với a và b là hai số đã cho và a ≠ 0 được gọi là phương trình bậc nhất một ẩn.
Hai quy tắc biến đổi phương trình
- Quy tắc chuyển vế
Trong một phương trình, ta có thể chuyển một số hạng từ vế này sang vế kia và đổi dấu số hạng đó.
Ví dụ: 3x + 4 = 0 ⇔ 3x = − 4
- Quy tắc nhân với một số
Trong một phương trình, ta có thể nhân cả hai vế với cùng một số khác 0.
Ví dụ: 3x = − 4 ⇔ 3.1/3 .x = − 4 .1/3 ⇔ x = – 4/3 (ta nhân cả hai vế với 1/3 cũng tương đương với việc ta chia cả hai vế cho 3)
Như vậy bài viết trên đây Truongkinhdoanhcongnghe đã hướng dẫn bạn phương pháp giải Phương Trình Đưa Được Về Dạng Ax B 0. Chúc bạn học tập tốt!
Xem thêm:
