

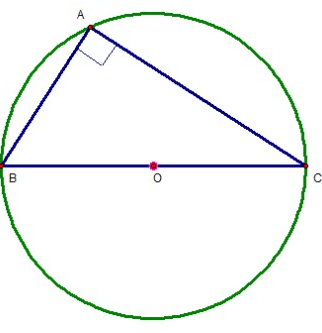
Tính chất đường tròn ngoại tiếp tam giác có những tính chất nổi bật và thường dùng nào thường xuyên được nhắc tới, thường xuyên phải sử dụng khi làm bài tập hình.
Nếu bạn đang ở trang này thì bạn sẽ chẳng phải lo sợ nữa, bởi trường kinh doanh công nghệ sẽ giúp bạn liệt kê toàn bộ những kiến thức giúp bạn giải những bài tập cần dùng tính chất Tam Giác Vuông Nội Tiếp Đường Tròn. Cùng theo dõi ngay dưới bài viêt này nhé!
| Theo định nghĩa, đường tròn ngoại tiếp của tam giác là đường tròn đi qua các đi qua tất cả các đỉnh của tam giác đó và tâm của đường tròn ngoại tiếp là giao điểm của ba đường trung trực của tam giác đó. |
+) Mỗi tam giác chỉ có duy nhất một đường tròn ngoại tiếp tam giác
+) Tâm đường tròn ngoại tiếp là giao điểm của 3 đường trung trực
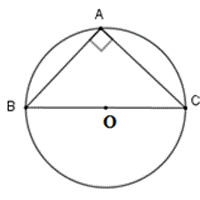
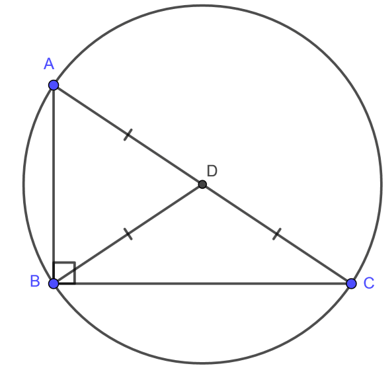
+) Tâm đường tròn ngoại tiếp của tam giác vuông là trung điểm của cạnh huyền
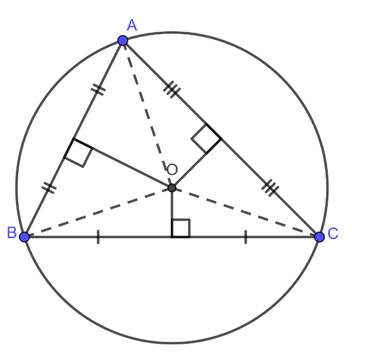
+)Trong tam giác đều, tâm đường tròn ngoại tiếp và nội tiếp trùng nhau
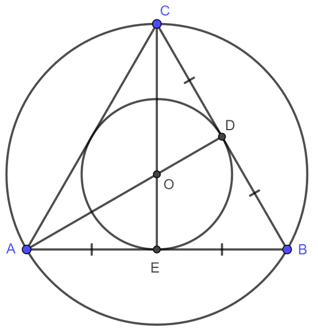

Có 2 cách giúp bạn xác định được tâm trong tam giác vuông:
+) Cách 1: Tâm của đường tròn ngoại tiếp của tam giác vuông là trung điểm của cạnh huyền ( ==>> Chứng minh tam giác vuông nội tiếp đường tròn )
+) Cách 2: Xác định tam giác đó có một cạnh là đường kính của đường tròn ngoại tiếp tam giác ==>> thì tam giác đó là tam giác vuông
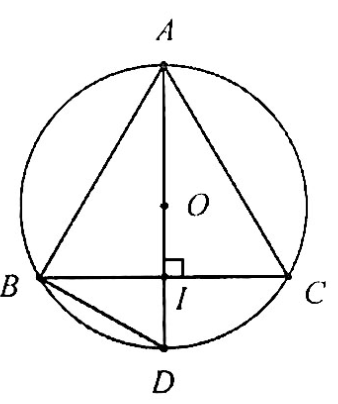
Giả xử tam giác đó là tam giác cân tại A
+) Tâm đường tròn ngoại tiếp của tam giác cân sẽ nằm trên đường cao, hạ từ đỉnh A xuống BC
+) Ta dựng đường trung trực của cạnh AB, đường này cắt đường cao hạ từ đỉnh A
=> Tại đây chúng giao nhau và ta đã xác định được tâm của đường tròn trong trường hợp của tam giác cân
Các công thức tính bán kính đường tròn ngoại tiếp tam giác:
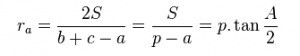
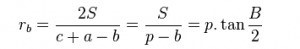
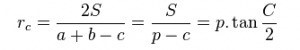
Trong đó:
Cách đầu tiên chính là sử dụng định lí sin trong tam giác để tính bán kính đường tròn ngoại tiếp tam giác.
Ví dụ: Cho tam giác ABC có BC = a, CA = b và AB = c, R là bán kính đường tròn ngoại tiếp tam giác ABC. Khi đó:
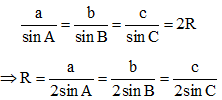
Trong đó có:
Bên cạnh cách dùng định lý sin, chúng ta cũng có thể sử dụng diện tích trong tam giác để tính bán kính đường tròn ngoại tiếp tam giác:
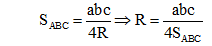
Trong đó có:
Ngoài ra, tính bán kính đường tròn khi sử dụng trong hệ tọa độ cũng là một cách được rất nhiều người ưa chuộng. Sau đây là các bước cơ bản để tính bán kính:
Sử dụng tam giác vuông để tính bán kính có lẽ là cách cơ bản nhất. Tâm của đường tròn ngoại tiếp trong tam giác vuông là trung điểm của cạnh huyền.
Do vậy, bán kính đường tròn ngoại tiếp tam giác vuông là bằng nửa độ dài của cạnh huyền đó.
Trên đây là những kiến thức liên quan về Tam Giác Vuông Nội Tiếp Đường Tròn mà truongkinhdoanhcongnghe tổng hợp được. Hi vọng bài viết hữu ích với bạn.
Xem thêm: