Tìm Tập Xác Định Của Hàm Số 12

Tìm Tập Xác Định Của Hàm Số 12 là một dạng toán thường xuyên xuất hiện trong đề thi. Mời bạn đọc cùng trường kinh doanh công nghệ tìm hiểu về phương pháp giải dạng toán này qua bài viết sau.

Tập xác định của hàm số là gì? Tìm Tập Xác Định Của Hàm Số 12

Trước hết các em cần phải hiểu thật chính xác tìm tập xác định của hàm số là gì? Tìm tập xác định có nghĩa là ta phải xét các điều kiện làm sao cho hàm số có nghĩa.

• Hàm số có chữa mẫu thì điều kiện để hàm số có nghĩa là mẫu phải ≠ 0.
• Hàm số có chứa căn thức thì biểu thức trong căn phải ≥ 0 để hàm số có nghĩa.
• Hàm số logarit có nghĩa khi biểu thức của loga ≥ 0
• Hàm số lũy thừa chia thành 3 trường hợp:

+ Nếu hàm số có mũ nguyên dương thì cơ số ∈ R

+ Mũ nguyên âm hoặc mũ = 0 thì cơ số phải ≠ 0

+ Mũ không nguyên thì cơ số phải > 0

Ví dụ chi tiết hướng dẫn Tìm Tập Xác Định Của Hàm Số 12

Hàm số logarit có dạng y = log_ax với a>0, a ≠ 1

Ví dụ: Tìm điều kiện của a hàm số log₆(2a-a²)

A. 0 < a < 2                                                     B. a>2

C. -1< a <1                                                      D. a < 3

Biểu thức log₆(2a-a²) xác định khi 2a-a²> 0 ⇔ 0<a<2

Ngoài cách giải tự luận trên, học sinh còn có thể sử dụng máy tính để tìm tập xác định của hàm số lớp 12.

Các bước làm như sau: Chọn a= 1 nhập log₆(2.1-1²) ta được kết quả = 0 tức là biểu thức có nghĩa.

⇒ Loại đáp án B, C.

Chọn a = -1 nhập tiếp log (2.(-1)1-(-1)1²), máy tính hiện MATH ERROR  biểu thức không có nghĩa nên loại D.

Vậy đáp án đúng ở đây là A.

Tìm tập xác định của hàm lũy thừa

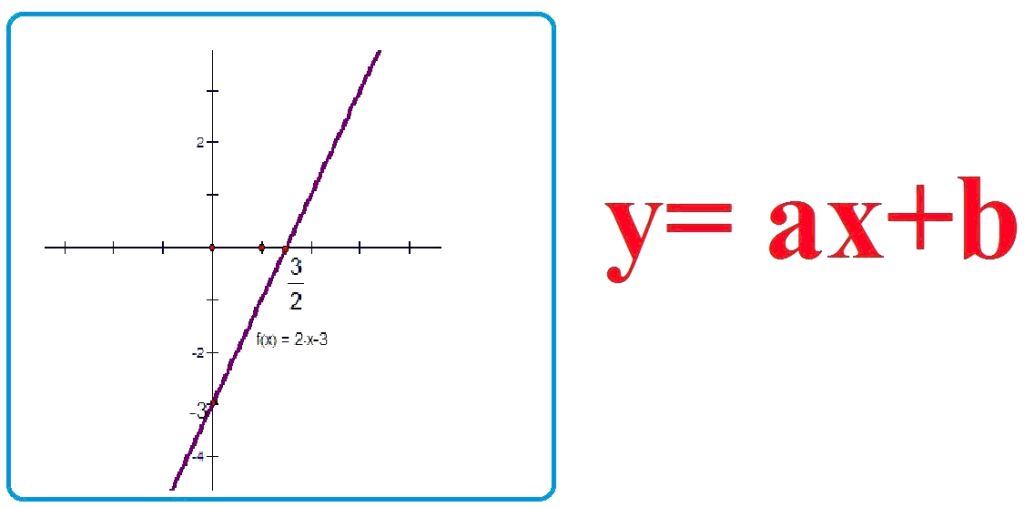
Trong câu hỏi tìm tập xác định của hàm số lớp 12, câu hỏi liên quan đến hàm số mũ là một trong những câu hỏi khó, học sinh rất dễ nhầm lẫn. Trước hết, học sinh cần ghi nhớ những kiến ​​thức sau:

Hàm lũy thừa y = x^α với α ∈ R hàm số mũ.

Tập xác định của hàm sẽ phụ thuộc vào giá trị của α.

Nếu:

• Nếu α là số nguyên dương thì D = R.
• α không nguyên thì D = (0; + ∞).

Vấn đề 1: Tập xác định của hàm số mũ và hàm số vô tỷ

Xét hàm y = [f(x)]^α

• Khi α là số nguyên dương: hàm được xác định khi và chỉ khi xác định f (x).
• Khi α là một nguyên âm: hàm được xác định khi và chỉ khi f (x) ≠ 0.
• Khi α không nguyên: hàm xác định khi và chỉ khi f (x)> 0.

Vấn đề 2: Tập xác định của các hàm lôgarit

• Hàm y = logaf (x) xác định

• Hàm y = logg (x) f (x) xác định

• Hàm y = (f (x)) g (x) xác định ⇔ f (x)> 0

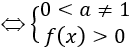
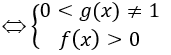
Như vậy bài viết trên Truongkinhdoanhcongnghe đã hướng dẫn các cách Tìm Tập Xác Định Của Hàm Số 12. Hi vọng những thông tin này hữu ích với bạn. Chúc bạn học tập tốt.

Xem thêm:

• Hai Mươi Lăm Hay Hai Mươi Năm?
• Giải Bài Toán Theo Tóm Tắt Lớp 3
• Bài Tập Toán Chuyển Động Lớp 5 Cùng Chiều
• Hàm Số Y Cosx Đồng Biến Trên Khoảng Nào?
• Cách Đọc Bảng Số La Mã Từ 1 Đến 30 Dễ Ghi Nhớ Nhất