Tìm hiểu cách tính logarit bằng máy tính một cách đơn giản và hiệu quả. Bài viết của trường kinh doanh công nghệ sẽ cung cấp cho bạn các bước chi tiết và hướng dẫn cụ thể để tính toán logarit một cách nhanh chóng và chính xác.
Logarit là gì? Cách Tính Logarit Bằng Máy Tính
Hàm logarit trong toán học chính là phép toán nghịch đảo của lũy thừa, hiểu 1 cách đơn giản hơn thì hàm logarit chính là đếm số lần lặp đi lặp lại của phép nhân.
Chẳng hạn như logarit cơ số 10 của 1000 chính là số 3, bởi vì theo phép tính nhân 10 x 10 x 10 tức là bằng với 10 mũ 3 chính là 1000.
Logarit có thể được dùng để tính toán cho bất kỳ 2 số dương thực a và b (trong đó a phải khác 0) bởi vì lũy thừa cho phép 1 số thực dương bất kỳ có thể lũy thừa với số mũ bất kỳ luôn cho ra 1 kết quả là số dương .
Ví dụ: Số logarit x là y = logax chỉ khi thỏa mãn được đẳng thức ay = x
Với
- x > 0; a > 0; a ≠ 1
- x – số logarit
- a – cơ số
- y – số mũ
Các công thức của Logarit:
Cách bấm máy tính Logarit
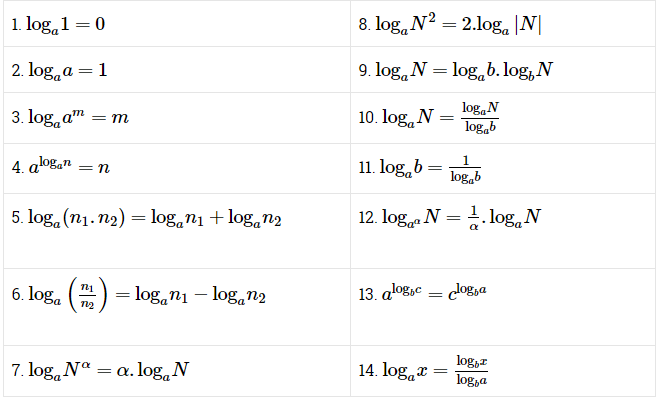
– Đối với Logarit thông thường
Bấm SHIFT + LogbX màu đen ở hàng thứ 2 ngoài cùng phía bên phải để bấm Log. Hàm số này có dạng LogbX vì vậy bạn cần nhập cơ số b trước, sau đó mới nhập Logarit của cơ số b (X) sau.
– Đối với Logarit tự nhiên
Bấm SHIFT + Ln, màu đen phím thứ ba từ trên xuống, ngoài cùng phía bên phải. Hàm số này có dạng Ln x, vì cơ số bằng e (~ 2,71828) đã được thiết lập sẵn trên máy nên bạn chỉ cần nhập Logarit của cơ số e thay vì nhập b như LogbX.
Cách giải phương trình Logarit bằng máy tính
– Giải phương trình Logarit trắc nghiệm
Bước 1: Chuyển phương trình về 1 vế > Nhập phương trình vào trong máy tính.
Bước 2: Bấm CALC thử lần lượt các đáp án A, B, C, D vào phương trình > Bấm “=” > Nếu kết quả bằng 0 thì đáp án đó là đáp án đúng.
Ví dụ: Phương trình Log2X Log4X Log6X = Log2X Log4X + Log4X Log6X + Log6X Log2X có tập nghiệm là:
A. {1}
B. {2,4,6}
C. {1,12}
D. {1,48}
Giải
Phương trình mới có dạng: Log2X Log4X Log6X – (Log2X Log4X + Log4X Log6X + Log6X Log2X) = 0. Nhập vào máy tính vế trái của phương trình.
Tại X = 1, ta bấm “CALC + 1 + =” > Phương trình = 0.
Vậy X = 1 là nghiệm của phương trình, chúng ta loại được đáp án B.
Tại X = 12, ta bấm “CALC + 12 + =” > Phương trình ra đáp án khác 0.
Vậy X = 12 không là nghiệm của phương trình. Loại đáp án C.
Tại X = 48, ta bấm “CALC + 12 + =” > Phương trình = 0.
Vậy X = 48 là nghiệm của phương trình.
Suy ra, đáp án D là đáp án đúng.
– Giải phương trình Logarit bằng tính năng SOLVE
Tính năng SOLVE trên máy tính cầm tay là tính năng cho phép giải nhanh để tìm nghiệm X bất kỳ, phù hợp với một số bài toán trắc nghiệm, cần giải nhanh. Tuy nhiên tính năng này không làm tròn được một số giá trị phức tạp, cũng như không rà được toàn bộ nghiệm phương trình.
Bước 1: Chuyển phương trình về 1 vế và nhập trực tiếp phương trình vào máy tính cầm tay.
Bước 2: Ấn SHIFT + CALC.
Ví dụ: Cho các số thực dương a, b thỏa mãn Log9(x) = Log16(a+12Log9x). Tính x.
Giải
Nhập phương trình Log9(x) – Log16(a+12Log9x) = 0 vào máy tính như hình dưới.
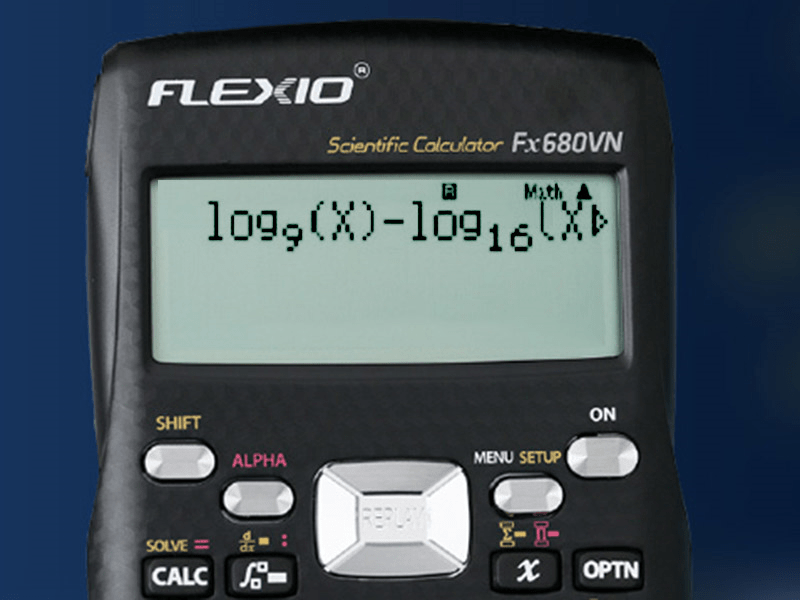
Bấm SHIFT + CALC.
Lưu ý: Khi máy tính hiện Solve for X? bạn có thể nhập giá trị X bất kỳ.
Tại đây máy sẽ cho ra một kết quả khá lẻ là 39.4622117. Tới bước này, đối với bài toán trắc nghiệm, bạn có thể so với từng đáp án đã cho để tìm ra đáp án đúng nhé.
– Giải phương trình Logarit bằng tính năng TABLE
Ví dụ: Tính tích các nghiệm của phương trình sau: Log3(3X) Log3(9X) = 4.
Bước 1: Bấm MODE > 7 > Nhập hàm số: f(x) = Log3(3X) Log3(9X) – 4.
Bước 2: Nhấn “=” > Chọn START = 0 > “=” > Chọn END = 29 > “=” > Chọn STEP = 1 > “=”.
Bước 3: Dò cột f(x) để tìm những khoảng hàm số đổi dấu. Ví dụ như hình dưới đây ta thấy khoảng (0;1) và (1;2) hàm số đổi dấu từ âm sang dương. Vậy trên khoảng này sẽ có khả năng có nghiệm, ta sẽ xét tiếp 2 khoảng này.
Bước 4: Bấm AC và dấu = để làm lại các bước trên. Với khoảng (0;1) ta chọn START = 0 > END = 1 > STEP 1/29. Ta được khoảng (0;0,0344) có thể có nghiệm, ta sẽ dò tiếp khoảng này để tìm nghiệm gần đúng nhất.
Bước 5: Với khoảng (0;0,0344) ta chọn START = 0 > END = 1 > STEP = 0,0344/29. Ta được nghiệm nằm trong khoảng (0,0189-0,0201).
Bước 6: Muốn có nghiệm chính xác hơn nữa ta lặp lại với START = 0,0189 > END = 0,0201 > STEP = (0,0201-0,0189)/29. Ta được nghiệm đúng thứ nhất là 0,01997586207.
Bước 7: Làm tương tự với khoảng (1;2). Ta được nghiệm đúng thứ hai là 1,852482759.
Bước 8: Bấm tích hai nghiệm với nhau ta thu được kết quả của bài toán.
Trên đây là những thông tin hướng dẫn Cách Tính Logarit Bằng Máy Tính. Truongkinhdoanhcongnghe hi vọng bài viết này hữu ích với bạn.
Xem thêm:
- Cách Chia 3 Chữ Số Cho 1 Chữ Số Chi Tiết Nhất
- Bảng Cộng Trừ Trong Phạm Vi 100
- Công Thức Tính Tổng Dãy Số Lớp 4 Dễ Nhớ Nhất
- Công Thức Tính Tổng Dãy Số Cách Đều Lớp 6
- Thế Kỉ XVI Là Thế Kỷ Bao Nhiêu?
Tốt nghiệp khoa sư phạm tiểu học, nhiều năm trực tiếp giảng dạy bậc tiểu học, cô rất hiểu tâm lý các em HS; lối truyền đạt kiến thức phù hợp với con trẻ. Với quan điểm “Giáo dục là vũ khí mạnh nhất để thay đổi cả thế giới” cô Huệ luôn cố gắng hết mình để truyền tải tri thức tới các em học sinh.
