Cách Tính Sai Số Tương Đối Chuẩn Xác Nhất

Trong bài viết dưới đây trường kinh doanh công nghệ sẽ hướng dẫn bạn đọc cách tính sai số tương đối nhanh và chuẩn xác nhất. Mời bạn đọc cùng theo dõi!

Chi tiết cách tính sai số tương đối

Sai số tương đối của số gần đúng a (được ký hiệu là δa) là tỷ số giữa sai số tuyệt đối và giá trị tuyệt đối của nó. 

Công thức tính sai số tương đối của phép đo là:

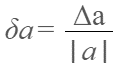
Thường sai số tương đối được biểu diễn dưới dạng % với 2 hoặc 3 chữ số. Nếu sai số tương đối δa hay da càng nhỏ thì chất lượng của phép đo đạc hay tính toán càng cao.

Sai số là gì? Cách Tính Sai Số Tương Đối

Sai số là sự khác biệt giữa giá trị đo được hoặc tính được và giá trị thật sự hay chính xác của một đại lượng nào đó. Khi đo đạc một đại lượng nào đó nhiều lần, dù có chú ý đến đâu thì kết quả của các lần đo cũng không giống nhau. Điều này cho thấy kết quả đo luôn chứa sai số và kết quả mà chúng ta thu được chỉ là giá trị xấp xỉ.

Sai số có nhiều nguyên nhân nhưng phổ biến nhất là do dụng cụ máy móc và kỹ năng của người đo không tốt. Một số yếu tố khác gây ra sai số là các ảnh hưởng của môi trường như gió, thời tiết,…”

Phân loại sai số

Sai số có thể chia thành 4 loại như sau:

• Sai số hệ thống

Sai số hệ thống là sai số do đặc tính của dụng cụ đo gây ra, đặc biệt khi điểm 0 ban đầu không chính xác mà ta không hiệu chỉnh trước khi đo.

Sai số dụng cụ ∆A’ có thể bằng nửa hoặc một độ chia nhỏ nhất trên dụng cụ đo.

Ví dụ: Nếu nhiệt độ cốc nước là 32,30C, mà ta dùng nhiệt kế có độ chia nhỏ nhất là 10C để đo thì ta chỉ có thể đọc được giá trị từ 320C đến 330C, không thể biết được phần lẻ. Đây là sai số do dụng cụ đo và không thể tránh được.

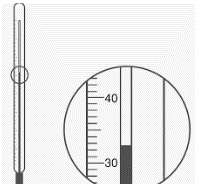
Nếu điểm 0 ban đầu bị sai lệch thì sai số càng lớn hơn. Ví dụ kim của vôn kế ban đầu không chỉ vạch số 0, khi đo sẽ cho kết quả sai. Sai số này có thể hiệu chỉnh được bằng cách đưa kim về vạch 0 ban đầu.

Ví dụ khác: Nếu ta dùng thước 20 mét để đo một đoạn thẳng nhưng chiều dài thật của thước lúc đó là 20,001m. Như vậy kết quả mỗi lần kéo thước sẽ sai 1mm. Đây là sai số hệ thống. Sai số hệ thống có hai loại là sai số hệ thống cố định và sai số hệ thống thay đổi.

• Sai số ngẫu nhiên

Khi đo cùng một đại lượng với cùng một dụng cụ đo nhiều lần, ta thường thu được các kết quả không giống nhau.

Sự khác biệt này không có nguyên nhân rõ ràng, có thể do cách thực hiện giữa các lần đo không đồng nhất, do giới hạn về khả năng quan sát của con người, do điều kiện thí nghiệm không ổn định, bị ảnh hưởng bởi các yếu tố ngẫu nhiên bên ngoài…. Sai số loại này được gọi là sai số ngẫu nhiên.

Sai số ngẫu nhiên của một phép đo đại lượng vật lý là trung bình cộng của sai số tuyệt đối của n lần đo.

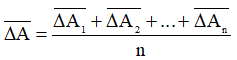
Ví dụ: Đo thời gian rơi của vật rơi tự do giữa hai điểm A và B trong các lần đo khác nhau thu được các giá trị khác nhau.

•  Sai số tuyệt đối

Nếu số gần đúng a có giá trị đúng là a0 thì ta nói a xấp xỉ a0 hay a là số gần đúng của a0. Khi đó sai số của a là

Ea= a-a0 (1.1)

Nhưng giá trị này nói chung ta không biết được mà chỉ ước lượng được cận trên của giá trị tuyết đối của nó.

Định nghĩa. Giá trị ước lượng Δa sao cho được gọi là sai số tuyệt đối của số gần đúng a.

| a-a0| ≤ Δa (1.2)

Sai số tuyệt đối nhỏ nhất có thể biết được gọi là sai số tuyệt đối giới hạn của a. Thông thường ước lượng sai số tuyệt đối giới hạn là rất khó và nhiều khi không cần thiết nên người ta chỉ cần ước lượng sai số tuyệt đối đủ nhỏ và dùng từ 1 đến 3 chữ số có nghĩa (là số chữ số bắt đầu từ chữ số khác không đầu tiên từ trái sang phải) để biểu diễn sai số tuyệt đối của số gần đúng.

Thay cho biểu thức (1.2) người ta còn dùng biểu diễn sau để chỉ sai số tuyệt đối:

a= a0 ± Δa (1.3)

Ví dụ: Một mảnh đất hình chữ nhất có chiều dài d=15,45m và chiều rộng r=3,94m với sai số 1cm. Khi đó ta hiểu là:

• Δd=0,01m hay d = 15,45m ± 0,01m
• Δr=0,01m hay r = 3,94m ± 0,01m

Khi đó diện tích của mảnh đất được tính là:

• S=d.r = 15,45 . 3,94 m = 60,873 m2

với cận trên là (15,45+0,01) .(3,94+0,01) = 61,067 m2

và cận dưới là (15,45-0,01) (3,94-0,01) = 60,679m2

hay 60,679 ≤ S ≤ 61,067

Vậy ước lượng sai số tuyệt đối của S là:

| S-S0| ≤0,194 m2 hay làm tròn 0,2 m2

• Sai số tương đối.

Hai số gần đúng có sai số tuyệt đối bằng nhau sẽ có “mức độ chính xác khác nhau nếu số độ lớn của chúng khác nhau. Số bé hơn sẽ có độ chính xác kém hơn.

Định nghĩa: Sai số tương đối của số gần đúng a (được ký hiệu là δa) là tỷ số giữa sai số tuyệt đối và giá trị tuyệt đối của nó:

Sai số tương đối của số gần đúng a (được ký hiệu là δa) là tỷ số giữa sai số tuyệt đối và giá trị tuyệt đối của nó. 

Công thức tính sai số tương đối của phép đo là:

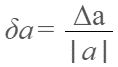
Dễ thấy:

Δa = |a| δa (1.5)

nên chỉ cần biết một trong hai loại sai số là tính được loại kia.

Ví dụ: Nếu a=57 và Δa = 0,5 thì δa= 0,0087719 hoặc 0,88%

Thường sai số tương đối được biểu diễn dưới dạng % với 2 hoặc 3 chữ số. Nếu sai số tương đối δa hay da càng nhỏ thì chất lượng của phép đo đạc hay tính toán càng cao.

Trên đây Truongkinhdoanhcongnghe đã hưỡng dẫn bạn Cách Tính Sai Số Tương Đối trong các đại lượng vật lý và một số ví dụ minh họa. Hy vọng những thông tin trên sẽ giúp ích cho bạn giải các bài tập. Chúc bạn học tập tốt!