Cách Tính Số Mũ Nhanh Và Dễ Hiểu Nhất

Trong bài viết dưới đây Truongkinhdoanhcongnghe sẽ chia sẻ tới bạn Cách Tính Số Mũ Nhanh và dễ hiểu nhất. Mời bạn đọc cùng theo dõi!

Cách tính lũy thừa nhanh nhất

Bình phương và nhân là thuật toán dùng để tính nhanh lũy thừa với cơ số tự nhiên. Thuật toán thường được áp dụng trong trường hợp cần tính lũy thừa và lấy dư theo một module nào đó.

Công thức truy hồi

Ý tưởng trên dẫn đến công thức sau:

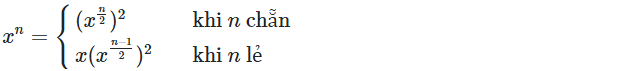
Độ phức tạp:

Do n giảm theo lũy thừa của 2 nên độ phức tạp của thuật toán là O(log n)

Cài đặt

Vì kết quả lũy thừa thường rất lớn nên ta sẽ tính phần dư khi chia cho MM. Khi cài đặt cần chú ý tránh tràn số.

Cài đặt đệ quy

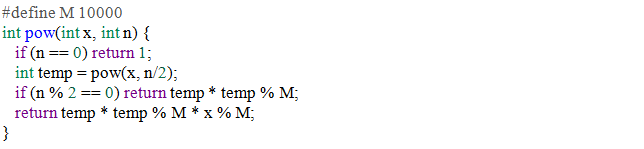
Cài đặt không đệ quy

Khái niệm lũy thừa

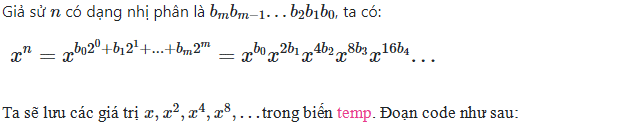
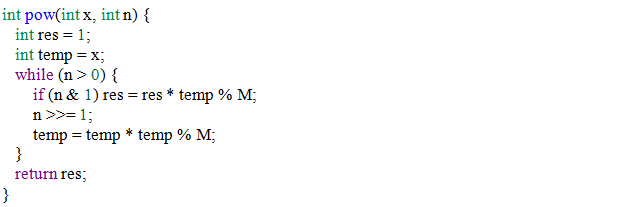
Lũy thừa là một phép toán hai ngôi của toán học thực hiện trên hai số a và b, kết quả của phép toán lũy thừa là tích số của phép nhân có b thừa số a nhân với nhau. Lũy thừa ký hiệu là ab, đọc là lũy thừa bậc b của a hay a mũ b, số a gọi là cơ số, số b gọi là số mũ.

Phép toán ngược với phép tính lũy thừa là phép khai căn. Lũy thừa có nghĩa là “nhân chồng chất lên”.

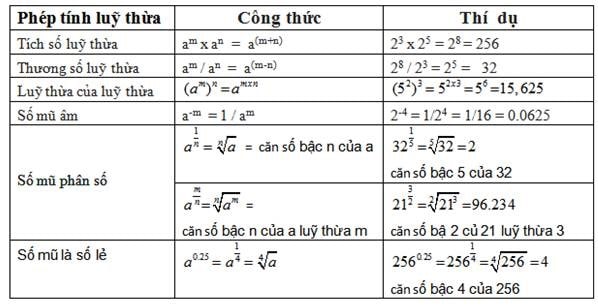
Lũy thừa 2 của a và lũy thừa 3 của a ngoài cách đọc thông thường còn có các cách đọc riêng.

a² ngoài cách đọc thông thường a lũy thừa 2, lũy thừa 2 của a hoặc a mũ 2 người ta còn đọc là a bình phương, hoặc bình phương của a

a³ ngoài cách đọc thông thường a lũy thừa 3 hoặc lũy thừa 3 của a hoặc a mũ 3 người ta còn đọc là a lập phương, hoặc lập phương của a

Lũy thừa của lũy thừa là gì?

Để hiểu được lũy thừa của lũy thừa là gì, chúng ta có thể suy ra từ định nghĩa của lũy thừa như sau:

Lũy thừa của lũy thừa là biểu thức lũy thừa trong đó phần cơ số là một biểu thức lũy thừa khác. Lũy thừa của lũy thừa có lý hiệu la (aⁿ)^m.

Công thức lũy thừa của lũy thừa

Công thức lũy thừa của lũy thừa (hay còn gọi là “công thức bình phương”) là một công thức trong đại số cho phép tính giá trị của một lũy thừa của một số đã được đưa lên một lũy thừa khác. Cụ thể, nếu ta có một lũy thừa có dạng a^(b^c), thì ta có thể tính giá trị của nó theo công thức:

a^(b^c) = (a^b)^c

Nói cách khác, ta có thể tính giá trị của lũy thừa b^c trước, sau đó lấy kết quả đó làm cơ số của lũy thừa a^x. Ví dụ, nếu ta muốn tính giá trị của 2^(3^4), ta có thể tính 3^4 trước, rồi lấy kết quả đó làm cơ số của lũy thừa 2^x.

2^(3^4) = 2^(81) = (2^3)^27 = 8^27

Do đó, giá trị của 2^(3^4) bằng 8^27.

So sánh hai lũy thừa cùng số mũ

a > b ⇒ aⁿ> bⁿ(n > 0)

Ví dụ: So sánh 4⁵ và 6⁵

Ta thấy 2 số trên có cùng số mũ là 5 và 4 < 6 ⇒ 4⁵< 6⁵

Ngoài ra, để so sánh hai luỹ thừa ta còn dùng tính chất bắc cầu, tính chất đơn điệu của phép nhân.

a < b thì ac < bc (c>0)

Ví dụ: So sánh 32¹⁰ và 16¹⁵, số nào lớn hơn.

Ta thấy các cơ số 32 và 16 khác nhau nhưng đều là luỹ thừa của 2 lên ta tìm cách đưa 32¹⁰ và 16¹⁵ về lũy thừa cùng cơ số 2.

32¹⁰= (2⁵)¹⁰= 2⁵⁰

16¹⁵= (2⁴)¹⁵= 2⁶⁰

Vì 2⁵⁰ < 2⁶⁰ ⇒ 32¹⁰< 16¹⁵

Trên đây là những thông tin hướng dẫn Cách Tính Số Mũ Nhanh nhất. truongkinhdoanhcongnghe hi vọng rằng bài viết này hữu ích với bạn.

Xem thêm:

Cách Tính Số Mũ Nhanh Và Dễ Hiểu Nhất

Share your love